A/B 测试

电商平台App AB Test

背景

某电商平台高度重视其产品详情页的优化工作，旨在通过页面设计的升级来提升用户转化效果。根据历史数据，该平台年度平均转化率维持在13%的水平，此次改版计划将转化率提升2个百分点，使目标值达到15%。为确保新版页面的实际效果，平台决定在全面上线前，先通过AB测试的方式对部分用户群体进行小规模验证，以评估新设计是否能够达成预期的转化目标。

AB Test 流程

分析现状，确定实验对象

实验开始前，我们需要与业务部门进行沟通确定实验的对象（实验变量）。此次项目中变量为 Web UI不同设计风格

确定实验目标和指标

此次实验需要确定新的UI界面是否能够提高2%的转化率，衡量指标就是 转化率

提出假设

这个AB测试，希望新的UI界面提升2%。

H0: P0 (旧UI设计转化率) = P1（新UI设计的转化率）

H1: P0 (旧UI设计转化率) $\ne$ P1（新UI设计的转化率）

原则上应该选用 右侧单位单尾检验；因为原则上假设 新UI转化率大于旧UI转化率。但是在这个实验中，我们不确定新UI的性能一定比当前的UI更好。

如果实验目的是验证新UI转化率是否明显高于旧UI，就可以选择单尾检验。但如果不确定两种设计是否存在差异，则应选择双尾检验

双尾检验 （Two-Tailed Test）

$H_{0} = \mu_{1} = \mu_{2} $

$H_{1} = \mu_{1} \ne \mu{2} $

单尾检验 （One-Tailed Test）

$H_{0} = \mu_{1} = \mu_{2}$

$H_{0} = \mu_{1} > \mu_{2} \text{ or } \mu_{1} < \mu_{2} $

实验分组 （流量分割）

确保实验组和对照组的样本分布均匀并具有随机性，从而最大程度减少其他因素对实验的结果干扰。

合理的样本分割需要遵循随机化原则，使实验组和对照组在性别、年龄、地区、设备类型、活跃程度等关键特征上尽可能保持一致。以避免系统性的偏差。通过这样的方式，可以确保实验期间，只有实验改动这一因素对核心指标产生影响，而其他无关变量被有效控制

合理的随机分组可以有效避免 辛普森悖论： 当数据被分组分析时，总体趋势可能会被分组内的特定趋势掩盖或逆转，从而得出错误的结论。这种现象往往是由样本分布不均匀导致的。

对照组：用户看到的旧UI的

实验组：用户看到的新UI的

Converted:0 代表用户在测试期间没有购买东西

Converted:1 代表用户在测试期间购买了产品

最小样本量

AB Test用最小样本来推断总体，总体分布可能有多种可能，可能是正态分布，可能是偏态分布。

根据 中心极限定理: 在样本量足够的情况下（>30），样本均值分布趋近于正态分布，正态分布曲线由均值和方差决定，该分布均值$E(-x)$趋近于总体均值$\mu$; 可以通过抽样，借助正态分布来估计置信区间，实现参数检验（t检验）

样本数量越大，估计约准确，但成本也就高，如何选定合适的最小样本数量

$$n=\frac{\delta^{2}}{\Delta^{2}}(Z_{\alpha/2} + Z\beta)^{2}$$

n为对照组和实验组各组所需要的样本量，总样本即为2n

σ为标准差

Δ为效应大小，指预期的两组差异幅度，在本项目中，Δ等于实验组的转化率减去对照组的转化率

α为犯第一类错误的概率，即弃真错误的概率。

𝛼=𝑃(拒绝 𝐻0∣𝐻0 为真)

β为犯第二类错误的概率，即纳伪错误的概率。

β=P(接受 H0∣H0 为假)

一般情况下我们设置：

显著性水平：α=0.05（或0.01）

统计功效（1−β）：β=0.2，即指检测到真实差异的概率，通常设为 0.8。在此案例中就是，如果新版落地页真的比旧版转换率要高，该测试有80%的概率能检测出这个状况。

当衡量指标为比率类指标时，标准差计算公式为：

$$\delta^{2} = P_{A}(1-P_{A})+P_{B}(1-P_{B})$$

借助在线工具求最小样本量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import statsmodels.stats.api as sms
import seaborn as sns

#计算效应大小，用于比较两个比例之间的标准化差异
effect_size = sms.proportion_effectsize(0.13,0.15)

#基于效应大小，功效，显著性水平，计算每组所需要的样本量
required_Minsamples = sms.NormalIndPower().solve_power(
    effect_size,
    power=0.8, #统计功效
    alpha=0.05,#显著性水平
    ratio=1,
)

np.ceil(required_Minsamples) #向上取整

n = 4720.0

实验周期

基于最小样本量 = 4720/组。我们现在有实验组和对照组，所以我们至少需要 4720 * 2 = 9440 个用户产于测试

如果UI界面每天平均浏览人数为1000， 则实验周期需要 9440/1000 = 9.4 约 10天

灰度测试

在正式开启的AB test 之前，为了确保实验的改动不会对系统或者对用户造成巨大的异常影响，通常需要先选取一小部分用户样本进行灰度测试，这样可以对少量用户的观察，评估实验改动点的风险和稳定性

通过灰度测试，可以验证实验的功能是否正常，用户体验是否符合预期，以及核心指标是否出现重大波动。如果灰度测试结果良好且风险可控，便可逐步扩大分流比例，最终进入正式的AB test 阶段；否者需要对实验方案或改动点进行调整，避免全面上线后带来不可控的负面影响

AB test线上和数据收集

根据确定好的实验方案，正式进行AB test, 同时通过特定的方法对核心指标进行监控，记录实验数据，便于后续分析

1
2
df = pd.read_csv('ab_data.csv')
df.head(5)

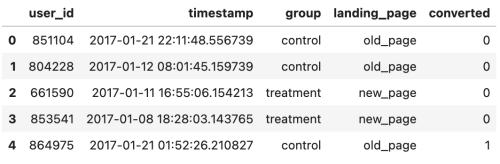
DataFrame

查看数据类型，以及是否存在缺失值

1
df.info()

Data Info

1
2
3
4
5
6
7
8
9
df.isnull().sum()

>>>>output:
user_id         0
timestamp       0
group           0
landing_page    0
converted       0
dtype: int64
1
2
3
4
5
6
7
8
9
10
11
12
13
14
cols = df.columns
for col in cols:
    print(f'{col} dupulicated: {df[col].duplicated().sum()}')

duplicated_userid = df[df['user_id'].duplicated()]['user_id']
df= df[~df['user_id'].isin(duplicated_userid)]


>>>>> output:
user_id dupulicated: 3894
timestamp dupulicated: 0
group dupulicated: 294476
landing_page dupulicated: 294476
converted dupulicated: 294476
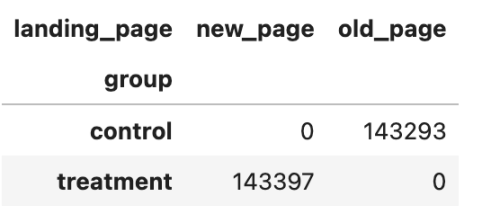
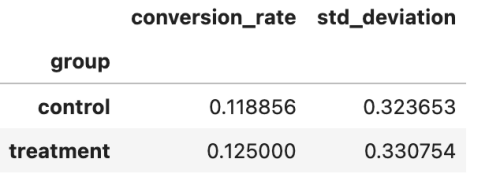
  • 查找分页和落地页不匹配的数据
  • 没有出现像重复user_id 记录中的分组和看到的页面不匹配的情况
1
pd.crosstab(df['group'], df['landing_page'])

Sample CrossTab

查看实验周期，要大于10天

1
2
3
df = df.copy()
df['timestamp'] = pd.to_datetime(df['timestamp']).dt.strftime('%Y-%m-%d')
len(df['timestamp'].unique())
  • 周期一共是23天，满足要求

进行抽样，根据之前我们得出的最小样本是4720

1
2
3
4
5
sample_size = 4720
control_sample = df[df['group']=='control'].sample(n=sample_size)
treatment_sample = df[df['group']=='treatment'].sample(n=sample_size)
sample_df = pd.concat([control_sample,treatment_sample],ignore_index=True)
sample_df

抽样结果

1
pd.crosstab(sample_df['group'],sample_df['landing_page'])

抽样后的Cross Tab

1
2
3
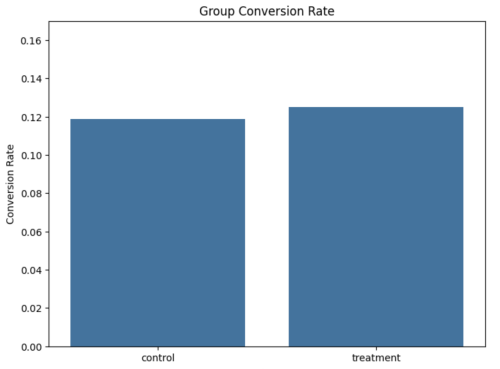
conversion_rates = sample_df.groupby('group')['converted'].agg([np.mean,np.std])
conversion_rates.columns = ["conversion_rate","std_deviation"]
conversion_rates

converstion_rate Cross Tab

1
2
3
4
5
6
7
plt.figure(figsize=(8,6))
sns.barplot(x=sample_df['group'],y=sample_df['converted'],errorbar=('ci', False))
plt.ylim(0,0.17)
plt.title("Group Conversion Rate")
plt.xlabel('group')
plt.ylabel('Conversion Rate')
plt.show()

图

假设检验

新旧版本的页面转化率是否相等进行检验，属于对比例进行检验，样本量足够大，总体方差未知，所以采用Z检验的方法，构造Z统计量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from statsmodels.stats.proportion import proportions_ztest,proportion_confint
control_num = sample_df[sample_df['group'] == 'control']["converted"]
treatment_num = sample_df[sample_df['group']=='treatment']["converted"]
cnt_control = control_num.count()
cnt_treat = control_num.count()
nobs = [cnt_control, cnt_treat]
successes = [control_num.sum(), treatment_num.sum()]

print(f"Nobs: {nobs}\n")
print(f"Successes: {successes}")

>>>>> OUTPUT:
Nobs: [np.int64(4720), np.int64(4720)]

Successes: [np.int64(561), np.int64(590)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#计算Z值 和 P值
z_stat, p_val = proportions_ztest(successes,nobs)
critical_value = stats.norm.ppf(1-0.025)
(lower_con, lower_treat),(upper_con, upper_treat) = proportion_confint(successes,nobs,alpha=0.05)

print(f"p_value : {p_val:.4f}")
print(f"Z_Statistic: {z_stat:.4f}")
print(f"临界值: {critical_value:.2f}")
print("落入拒绝域拒绝原假设，两版本存在差异" if abs(z_stat)>critical_value else "接受原假设，两版页面不存在差异")
print(f"95% for Control Group : [{lower_con:.3f},{upper_con:.3f}]")
print(f"95% for Control Group : [{lower_treat:.3f},{upper_treat:.3f}]")

>>>> OUTPUT:
p_value : 0.3617
Z_Statistic: -0.9122
临界值: 1.96
接受原假设，两版页面不存在差异
95% for Control Group : [0.110,0.128]
95% for Control Group : [0.116,0.134]

结果

P-val: 0.3671 高于显著水平 0.05, 并且Z统计量也是在接受域，也就是新旧版本页面转化率并没有显著不同

参考

参考文章